In the first installment of "A computer from scratch", I've built a NAND gate. In the third part I've built NOT, AND and OR circuits and I've also introduced the 4011 CMOS NAND gates, which I'm using instead of a bunch hand built, transistor-based NANDs (because hey, that's a lot of wiring, but not a lot of new insight). NOT, AND and OR circuits are built with one, two and three NANDs respectively.

In this part, I'll first build a XOR gate, which uses four NANDs, and then a half adder, which uses six NANDs.

At that point I'll build a full adder, but I'll start using pre-build XORs and ANDs for that, because that would be too many components to wire.

The results

All these build were easy, I've done them in minutes (well, without counting the time to find the right resistors but, ...yeah)

XOR gate

A NAND=based implementation of XOR can be built with four NANDs using the following identity (keep in mind that NOT X OR NOT Y = X NAND Y):

A XOR B = (A AND NOT B) OR (B AND NOT A)
        = NOT (A NAND NOT B) OR NOT (B NAND NOT A)
        = NOT (A NAND B NAND B) OR NOT (B NAND A NAND A)
        = (A NAND B NAND B) NAND (A NAND B NAND A)

Which can be implemented via this gate logic

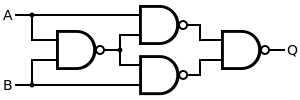
I've implemented this with a 4011 and the following plan

The build was easy and looked like this

Half Adder

Half adders start to become more interesting, they do sums! They have 2 ins and 2 outs and respect the following truth table:

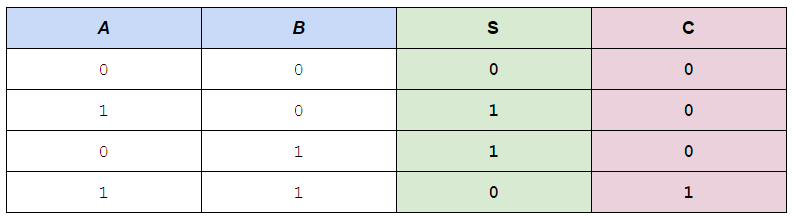
What they do is, given two bits (one in A and the other in B) they return the sum in S and the eventual overflow in C (for carry)

It's evident from the truth table that, S = A XOR B and C = A AND B and thus a half adder can be implemented via the following gate logic:

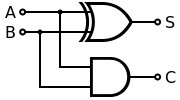
Since I had the previous build handy, I added an AND gate to the XOR gate I already had and got the following NAND-based half adder:

When laid out as a circuit and on a breadboard plan it looks like this

As you can see, stuff is getting complicated here! Here's the build

The board is getting pretty crowded...

Full adder

A full adder is a 3-in 2-out circuit which works like an adder. In addition to it, it has a carry in input, as well as output (so it adds 3 bits). It's a very important feature! Unfortunately, this makes the circuit much more complex. Here's the truth table

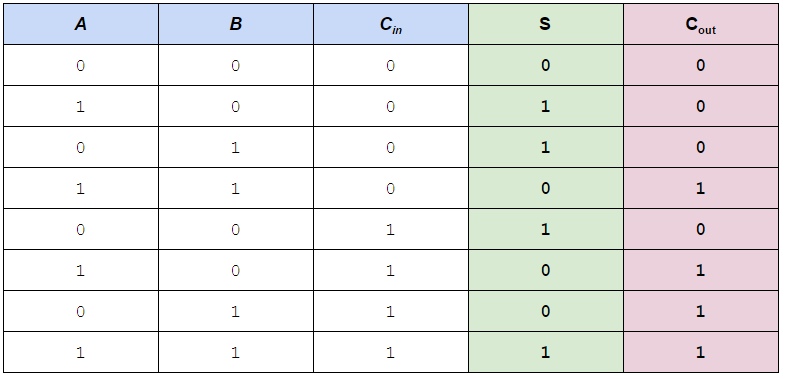
By looking at the parts where C_in has different values separately, I could recognize these identities

S     = C_in XOR (A XOR B)
C_out = C_in AND (A XOR B) OR (A AND B)

Reasoning on these, and looking at the half adder logic, if we start by connecting A and B to a half adder, we have in output

S_h1 = A XOR B
C_h1 = A AND B

We can then connect another half adder to C_in and S_h1 and obtain

S_h2 = S_h1 XOR C_in = C_in XOR (A XOR B)
C_h2 = S_h1 AND C_in = C_in AND (A XOR B)

Therefore S_h2 is the S output of the full adder, and we can also obtain C_out easily by ORing the two partial carries.

C_h1 OR C_h2 = A AND B OR C_in AND (A XOR B) = C_out

In summary, we need two half adders and an OR gate to build a full adder:

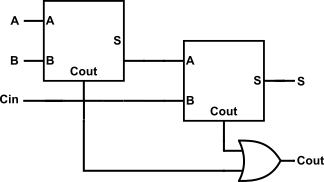
By substituting in the plans we already have for half adders and OR gates, we can derive a 15 NAND gate circuits. It's a tad too complex, so I'm cheating again by introducing three new friends: a 4-AND IC, a 4-OR IC and a 4-XOR IC.

This will allow me to use actual AND/OR/XOR gates in the diagram instead of NANDs. With this improvement, the diagram looks like this (stolen from Wikipedia):

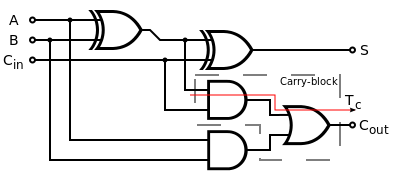
As you can see, only 2 XORs, 2 ANDs and 1 OR are necessary to build this. But first, let me introduce my new chips.

XOR (4070)

The 4070 is similar to a 4011 but performs four XORs instead of four NANDs. Its pinout is the following:

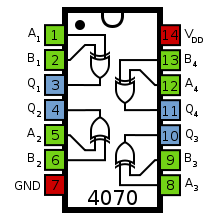
A₁ and B₁ will contain A and B; A₂ and B₂ will contain C_in and A XOR B, which we can pick up from Q₁. The output of this second gate is the sum S

AND (74HC08)

The next component I'll use is a 74HC08, which is performs 4 ANDs. It's not from the 4000 series but from the 7400 series. The only difference I can see is the layout of the inputs. In this case it looks like this:

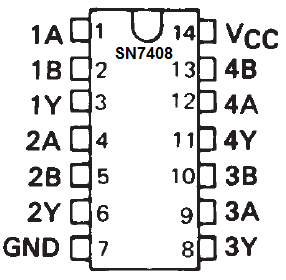
Following our diagram, we'll connect A and B to 1A and 1B; C_in and A XOR B (which is in Q₁ from before) to 2A and 2B respectively.

OR (4071)

The 4071 is a 4000 series 4 OR gate. It's pinout is similar to the 4011 and 4070 IC I used before.

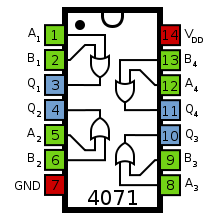
We need to OR the two partial carries coming out of the AND gate, and so we'll connect 1Y and 2Y to A₁ and B₁ and get C_out in Q₁.

The plan

Overall the circuit looks like the following schematic. You can download a better looking PDF as well.

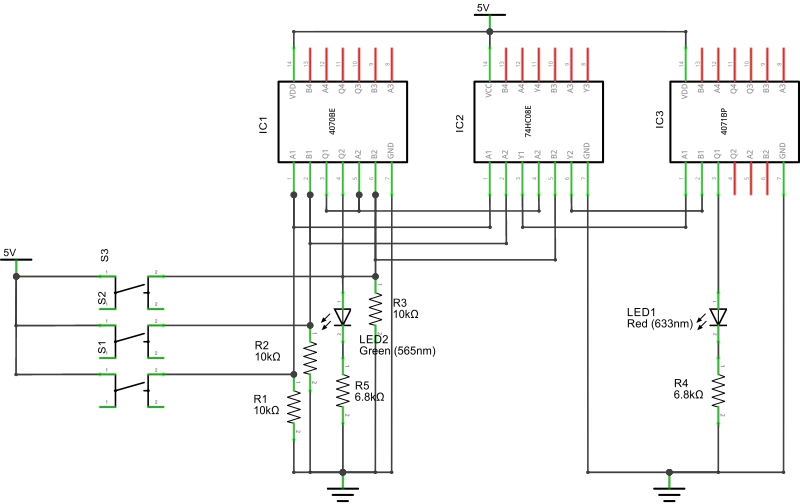
Note that I've deliberately left the top side of of the IC without any connection, beyond power. This will allow me, with relatively little work, to reuse this circuit to implement a second adder in the next part of this blog series. The breadboard plan is the following:

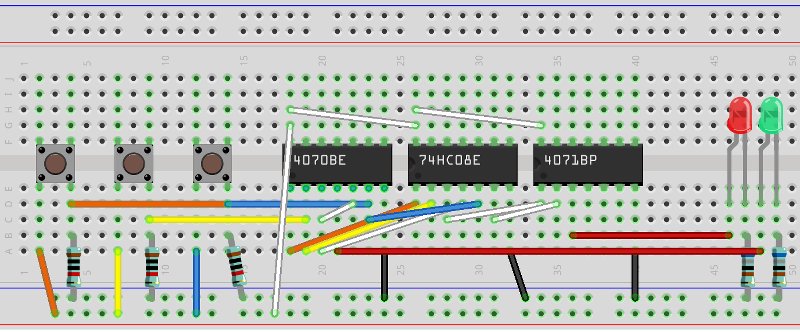
The three switches are A, B, and C_in, respectively. The red led is C_out and the green led is S.

The result

It works! It's a small thing but it's the first circuit I've built which actually does "something" not trivial. Before I started I had not figured out that addition and carry can be expressed as a truth table. Now I know, and my circuit does (very very simple) sums. I'm satisfied.

Next Steps

The next steps will be to build a 2-bit "ripple carry" adder and start investigating multiplexers. With those I will be very close to my next big step: building an ALU.

Resources

• I've used the program Fritzing to plan the circuits
• The Full Adder schematic to use with Fritzing.