As part of Stack Overflow's pro-diversity initiatives, I have been helping Andela by mentoring one of their fellows, Bosun, in data structures and algorithms. In the Stack Overflow "default open" style, I am putting some of our notes on the internet, in the hope they will be useful to more people. Most of the code is either pseudo-code or JavaScript, which we chose because it's simple and easy to access and everyone pretty much knows the basics of it.

Andela notes index

1. Iterators (part 1)
2. Iterators (part 2)
3. Stacks
4. Queues
5. Implementing a calculator (part 1)
6. Implementing a calculator (part 2)
7. Trees & Graphs
8. Compression: RLE encoding and decoding
9. Compression: Huffman encoding (part 1)
10. Compression: Huffman encoding (part 2) & decoding

In bold the current part, links point to the other available parts, in italics the parts not yet available.

A disclaimer

IANACS! A lot of the following may feel wrong, simplistic or offensive to Erlang tinkerers. That's because I am a self-taught nightmares' investigator, and not one of those Mr. No fanbois. If you encounter any problem, ask your parents if this content is suitable for your programming religion.

Intro

Queues and Stacks are very basic data structures. While JavaScript arrays are both queues and stacks (amongst other things), and we do not need to re-implement these, we are going to do so anyways.

• because it allows us to explore what queues and stacks do
• because it's interesting to know some algorithms which might be useful even though we never have to implement a queue or stack

Remember: you'll rarely encounter a situation where you need to implement a data structure exactly. In most cases, you'll need to know how data structures and algorithms work, in order to derive your custom variant to solve the problem at hand.

Both queues and stack are storage data structures. They have a method for inserting data (push for stacks and enqueue for queues), and a method for retrieving data (pop for stacks and dequeue for queues). Where they differ is the order in which elements are retrieved.

Stacks

Stacks are last-in, first-out structures (LIFO). This means that if you store three elements (A, B and C) you will retrieve them in the same opposite order (C, B and A). They are objects with two main methods

void push( item ); // stores "item" in the stack
<item> pop();      // retrieves "item" from the stack

Another often useful method is something that tells us if the stack has anything to read. In many cases it's not necessary, though

bool canRead();       // is there something in the stack?

What's cool about them

Stacks are extremely useful and in fact they are in use everywhere. They are used in cases where you need a shared data storage solution where the data is protected by scoping rules.

A scope a set of instructions (e.g. a method) which store and retrieve some values. Let's say a procedure needs to store and retrieve three values, a, b, c. It will therefore have an execution like this:

begin scope ThisIsAScope
store(a);
store(b);
store(c);

// some more code

retrieve(a);
retrieve(b);
retrieve(c);
return;
end scope

Assuming we are using a stack, which is a last in first out structure, we need to retrieve the elements in the opposite order as we stored them. We can also use pop and push instead of retrieve and store just to be coherent.

begin scope ThisIsAScope
push(a);
push(b);
push(c);

// some more code

pop(c);
pop(b);
pop(a);
return;
end scope

Why don't we use a first in first out structure and get rid of that pesky reverse order thing? The reason becomes apparent when we hypothesize that int the // some more code section there is another nested scope, for example procedure InnerScope, which needs to store d and e. Remembering that our storage is shared, and the following represents the execution of our code, so the other procedure in this notation is inlined, like the sequence of steps when debugging:

begin scope ThisIsAScope
push(a);
push(b);
push(c);

// some code

invoke(InnerScope)

    begin scope InnerScope
    push(d);
    push(e);

    // some more code

    pop(e);
    pop(d);

    return;
    end scope

// even moar code    

pop(c);
pop(b);
pop(a);
return;
end scope

Suppose for a moment that we were to use a first in, first out structure here. What would happen is that in order to retrieve d and e we'd have to remove a, b and c from storage, then take d and e, and then put back a, b and c. That's clearly not possible to do inside the inner scope for two reasons: firstly, the inner scope cannot know how much stuff it needs to remove before getting to its own values -- keep in mind that a procedure might be called by different callers! -- and secondly because it would violate the concept of scoping, imagine the mess if along with a call you'd pass all your variables!

This "clean up" process needs to be done, therefore, before calling and at each call. That is possible but impractical: it would be slow and error prone. Instead, with stacks, everything is simple, each scope only cares about its own storage and can freely ignore the rest of the universe... as long as it pops as many values as it pushes!

What follow are a two less abstract examples of this usage.

Simple calculators

Let's say you want to calculate the result of (1 + 2) * 4. This can be expressed in Reverse Polish Notation (each operator follows its operands) as 1 2 + 4 *. You can do so with a stack using the following convention: numbers are pushed on the stack, operators pop their operands and push their results on the stack. For example, going through the RPN expression one item at a time:

• 1 is a number, so we push it

  push( 1 );

• 2 is a number, so we push it

  push( 2 );

• + is an operator, we pop two operands, sum them, and push the result

  push( pop() + pop() ); // pops 2, pops 1, pushes 3

• 4 is a number, so we push it

  push( 4 );

• * is an operator, we pop two operands, multiply them, and push the result

  push( pop() * pop() ); // pops 4, pops 3, pushes 12

At the end, the result is the next value in the stack.

Machine Code

In machine code, subroutines are called by pushing parameters on the stack, and calling the subroutine address (a call means pushing the return address and then jumping). The subroutine will pop its operands, do its business, and return (a ret means popping the stack in the program counter, thus jumping to the address on the top of the stack).

// Main
// Call the subroutine at address 0x2000 with a single parameter of 0x0023

0x1000  MOV AX, 0x0023  // put the value of the parameter in AX
0x1003  PUSH AX         // push AX on the stack
0x1004  CALL 0x2000     // call the subroutine (push 0x1007 on the stack, 
                        // jump to 0x2000)
0x1007  ...             // etc.

...

// Subroutine
0x2000  POP BX          // retreive the parameter (0x0023) and put it in BX 
0x2001  ...             // do something with BX etc.

...

0x2034  RET             // pop 0x1007 in the register that holds the 
                        // next instruction to read (basically, jump 
                        // back to 0x1007)

Reversing lists and swapping items

Stacks can be used to swap items and reverse lists very easily: going from A-B-C to C-B-A can be done with

push(A);
push(B);
push(C);
pop();    // C
pop();    // B
pop();    // A

Let's code!

Stacks can be implemented with a fixed size array and an index pointing to the next available slot in it. They have two operations, pop which decreases the index and returns the element at the new value (this can throw a stack underflow exception if we try to read over the beginning of the array), and push which stores a value and increases the index (this can throw a stack overflow exception if we try to write over the end of the array. Furthermore a canRead method is often useful to determine the end of the stack.

Let's implement this in javascript, shall we? Bare using of array is verboten for the purposes of this exercise!

function () {
    var buffer = [];
    for (var i = 0; i < 50; i++) {
        buffer[i] = 0;
    }

    var top = -1;
    var self = {};

    // push adds something to the buffer
    self.push = function (item) {
        // your code here
    };

    // pop takes something from the buffer
    self.pop = function () {
        // your code here
        return null;
    };

    self.canRead = function () {
        // your code here
    };

    self.dump = function () {
        for (var i = 0; i <= top; i++) {
            var entry = i + ": " + buffer[i] + " ";
            if (top == i) entry += "T";
            console.log(entry);
        }
    };

    return self;
};

I've put together a project on GitHub which you can clone and complete. It already has tests and solutions if you want to cheat -- but I'd advise you at least try to implement these operators yourself for max enjoy.

How to set up your system

1. Install a recent version of node.js (link)
2. Fork https://github.com/sklivvz/andela-data-structures on github
3. Clone in your preferred folder
4. From a terminal npm install restores the test package
5. npm update && npm start 3 runs the code (note, update is necessary only the first run)

You should get something like

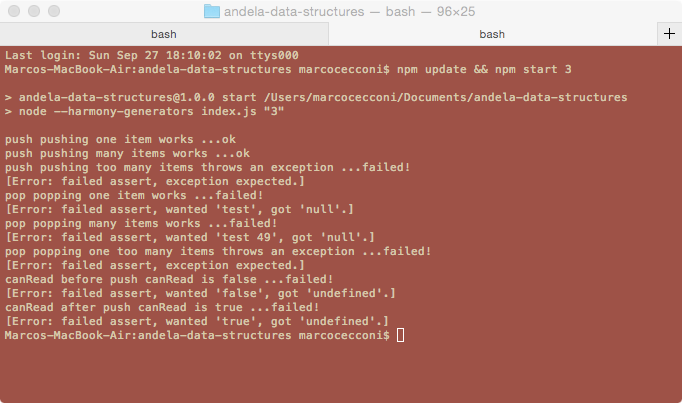
Edit the file ./parts/03-stacks.js with your solution and run again until all tests pass.

---

External links:

• Wikipedia on stacks